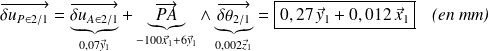Torseur des petits déplacements
Définition
La prise en compte des jeux lors du contact entre deux solides
et
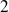autorise des mouvements supplémentaires de faible amplitude : on parle de petits déplacements. Ces petits déplacements autorisés par la liaison réelle (
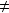liaison parfaite) sont modélisés par un torseur : le torseur des petits déplacements.
Définition : torseur des petits déplacements
On définit donc le torseur des petits déplacements du solide 2 par rapport au solide 1 :
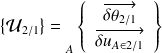
La résultante
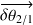est appelée vecteur petite rotation de 2 par rapport à 1.Le moment
est appelé vecteur petit déplacement de 2 par rapport à 1 au point A.
Complément : Démonstration
Les éléments de réduction peuvent être obtenus à partir de ceux du torseur cinématique
.
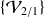Soient un solide 2 en mouvement par rapport à un autre solide 1 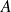et
et
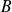sont deux points quelconques appartenant à 2.
On a :
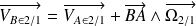
Soit
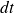un intervalle de temps élémentaire. On peut alors écrire :
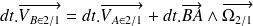
On pose alors :
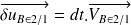et
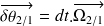
Ce qui revient à dire que les points
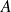et
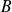se déplacent en ligne droite (voir figure ci-dessous). Ce n'est pas vrai pour un mouvement de grande amplitude, mais si le déplacement du solide est faible, cette approximation est très pertinente.
On a donc la relation :
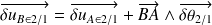
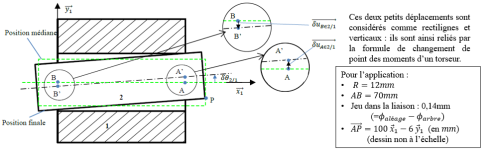
Application au guidage cylindrique
Objectif : déterminer l'angle d'inclinaison de l'arbre
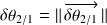ainsi que le vecteur petit déplacement du point P
.
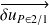Calcul de
:
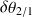La relation entre les petits déplacements de A et de B s'écrit :
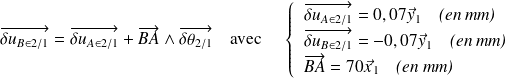
Ce qui donne :
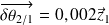(en radians) , c'est-à-dire :
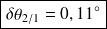
Pour le déplacement du point P, on se sert du petit déplacement du point A qui peut être déterminé à partir du jeu fonctionnel de la liaison :
